Gerak Harmonik Sederhana (Ghs)

Selamat tiba di softilmu, blog sederhana yang menyebarkan ilmu pengetahuan dengan penuh keikhlasan. Kali ini kami akan menyebarkan ilmu ihwal Gerak Harmonik Sederhana, beberapa poin utama yang akan kami bahas yakni Pengertian Gerak Harmonik Sederhana, Jenisnya, Besarannya, Simpangannya, Rumusnya, Kecepatan, Energi, Aplikasi, dan Contoh Soal Gerak Harmonik Sederhana. Semoga sanggup bermanfaat J

Gerak harmonik sederhana tak pernah luput dari pembelajaran pada masa sekolah menengah maupun jenjang perkuliahan. Jika dihubungkan dengan konsep kehidupan sehari-hari juga gerak harmonik sederhana memegang peranan penting. Pengaplikasian  

A. PENGERTIAN GERAK HARMONIK SEDERHANA

Salah satu jenis gerakan yang paling sederhana disebut gerak harmonik sederhana (GHS) atau simple harmonic oscillation (SHO). Mengapa dinamakan Harmonik sederhana? Sesuai dengan pengertian perkatanya yaitu harmonik yang artinya bentuk/pola yang selalu berulang pada waktu tertentu dan sederhana diartikan bahwa anggapan tidak ada gaya disipasi, sehingga amplitudo dan energi tetap/kekal

Gerak Harmonik Sederhana  adalah gerak periodik bolak balik dengan lintasan yang ditempuh selalu sama (tetap) berpusat pada satu titik (titik setimbang). Gerak Harmonik Sederhana mempunyai persamaan gerak dalam bentuk sinusoidal dan dipakai untuk menganalisis suatu gerak periodik tertentu. Gerak serasi sederhana yang sanggup dijumpai dalam kehidupan sehari-hari yakni getaran benda pada pegas dan getaran benda pada ayunan sederhana.

B. JENIS GERAK HARMONIK SEDERHANA

Gerak Harmonik Sederhana sanggup dibedakan menjadi 2 jenis, yaitu :

• Gerak Harmonik Sederhana Linier, pergerakannya ada pada satu garis lurus vertikal maupun horizintal. Misalnya penghisap dalam silinder gas, gerak osilasi air raksa / air dalam pipa U, gerak horizontal / vertikal dari pegas (pegas pada mobil), dan sebagainya.

GERAK HARMONIK SEDERHANA LINIER

• Gerak Harmonik Sederhana Angular, pergerakannya mengayun membentuk teladan setengah bulat ataupun sanggup saja perputaran. Misalnya gerak bandul/ bandul fisis(bandul jam), osilasi ayunan torsi, dan sebagainya.

GERAK HARMONIK SEDERHANA ANGULAR

C. BESARAN GERAK HARMONIK SEDERHANA

Besaran fisika pada Gerak Harmonik Sederhana pada pegas intinya sama dengan ayunan sederhana, yakni terdapat periode, frekuensi dan amplitudo. Jarak x dari posisi setimbang disebut simpangan. Simpangan maksimum alias jarak terbesar dari titik setimbang disebut amplitudo (A). Satu getaran Gerak Harmonik Sederhana pada pegas yakni gerak bolak balik lengkap dari titik awal dan kembali ke titik yang sama.

1. Perpindahan

Bola mulai dari sumbu x pada x = +A dan bergerak menempuh sudut θ dalam waktu t. Karena gerak ini merupakan gerak melingkar beraturan, maka bola bergerak dengan laju sudut konstan w (dalam rad/s). Akibatnya sanggup dinyatakan, θ = wt. Perpindahan bayangan pada arah x yakni proyeksi jari-jari bulat A pada sumbu

2. Periode (T)

Waktu yang dibutuhkan oleh benda yang bergerak harmonik sederhana untuk menempuh satu putaran penuh disebut perioda. Besar perioda bergantung pada laju sudut bola ω. Semaik besar sudut, semakin singkat waktu yang dibutuhkan untuk menempuh satu putaran.

Hubungan antara ω dan T diperoleh dari ω = Δθ/Δt, sehingga :

3. Frekuensi (f)

Selain periode, terdapat juga frekuensi alias banyaknya getaran yang dilakukan oleh benda selama satu detik. Frekuensi memperlihatkan seberapa “cepat” Gerak Harmonik Sederhana berlangsung, dalam grafik y-t frekuensi yang lebih besar ditunjukkan dengan grafik sinusoidal yang lebih rapat.

Pegas :

Bandul :

4. Amplitudo (A)

Amplitudo yakni perpindahan maksimum dari titik kesetimbangan.

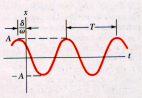AMPLITUDO

Sebuah pegas bila ditarik atau ditekan dari posisi normalnya akan melawan dengan gaya tertentu untuk menormalkan dirinya. Gaya ini disebut gaya pemulih (restoring force), yang besarnya sebanding dengan seberapa besar kita menarik/menekan pegas tersebut dan arahnya berlawanan dengan arah tarikan kita. Hubungan ini dirumuskan oleh Robert Hooke:

Artikel Penunjang : Pengertian, Konsep,Rumus, dan Aplikasi Hukum Hooke

D. SIMPANGAN GERAK HARMONIK SEDERHANA

Simpangan gerak harmonik pada suatu titik merupakan jarak titik tersebut ke titik seimbang.

Atau

Dimana :

Y = simpangan gerak harmonik (m)

A = amplitudo (m)

ω = kecepatan sudut (rad/s)

T = periode getaran (s)

F = frekuensi getaran (Hz)

t = waktu tempuh (s)

E. KECEPATAN GERAK HARMONIK SEDERHANA

Berbeda dengan simpangan yang menunujukkan posisi suatu benda, maka kecepatan merupakan turunan pertama dari posisi.

Nilai kecepatan v maksimum ketika cos ωt = 1, sehingga kecepatan maksimumnya yakni :

Lalu, kecepatannya di sembarang posisi y atau korelasi kecepatan dengan simpangan harmonik yakni :

F. PERCEPATAN GERAK HARMONIK SEDERHANA

Percepatan sanggup dicari dengan mengingat bahwa percepatan yakni turunan pertama kecepatan terhadap waktu.

Nilai percepatan (a) akan maksimum pada ketika sin ωt = 1, sehingga percepatan maksimumnya yakni :

Hubungan percepatan dengan simpangan harmonik :

Artikel Penunjang : GLB dan GLBB

G. ENERGI PADA GERAK HARMONIK SEDERHANA

Gerak Harmonik Sederhana tidak hanya mempunyai persamaan-persamaan, tetapi juga energienergi yang membarenginya. Apa saja energi  itu?

1. Energi Kinetik

Energi kinetik yakni energi yang dimiliki oleh benda yang melaksanakan gerak harmonik sederhana alasannya yakni kecepatan geraknya.

Energi kinetik maksimum pada gerak harmonik dicapai ketika berada di titik setimbang. Sedangkan energi kinetik minimum dicapai ketika berada di titik balik.

2. Energi Potensial

Besarnya energi potensial yakni energi yang dimiliki gerak harmonik sederhana alasannya yakni simpangannya. Secara matematis energi potensial yang dimiliki gerak harmonik dirumuskan sebagai berikut :

Energi maksimumnya terjadi pada gerak yang dicapai ketika berada di titik baliknya.

3. Energi Mekanik

Energi ini merupakan hasil penjumlahan energi kinetik dan potensial.

Berdasarkan persamaannya, energi mekanik suatu benda yang bergerak harmonik tidak bergantung waktu dan tempat. Jadi, energi mekanik sebuah yang bergerak dimanapun besarnya sama.

ENERGI MEKANIK

Semua benda yang bergetar di mana gaya pemulih F berbanding lurus dengan negatif simpangan (F = -kx), maka benda tersebut dikatakan melaksanakan gerak harmonik sederhana (GHS) alias Osilator Harmonik Sederhana (OHS).

Artikel Penunjang : Pengertian, Rumus dan Aplikasi Hukum Gravitasi

H. APLIKASI GERAK HARMONIK SEDERHANA

Pengaplikasian gerak harmonik cukup banyak dalam kehidupan berupa alat bantu manusia. Berikut beberapa aplikasinya :

1. Shock Absorber (pegas)

Peredam kejut pada kendaraan beroda empat mempunyai komponen pegas yang terhubung  pada piston dan dipasangkan erat roda kendaraan. Hal ini membantu untuk mengendalikan atau meredam guncangan pada roda.

2. Jam bandul

Karena tidak memakai baterai, jam bandul bekerja dengan memanfaatkan tenaga gravitasi atau pegas. Baik jam pegas atau jam rantai mempunyai prosedur pemutar dan terdapat roda gigi yang berputar dan menggerakkan jarum jam ibarat halnya bandul yang bergerak kekiri dan kekanan.

3. Pita elastis

Berkalu ibarat pegasmirip dengan sistem massa pegas. Keduanya akan bergetar dari titik setimbangnya sampai gaya goresan mengeluarkan daya redam. Strukturkaret membuatnya mempunyai energi potensial lentur yang tinggi sehingga sanggup diaplikasikan ke penggunaan kabel bugee jumping.

4. Trampolin

Bahan trampolin merupakan pegas yang tingkat elastisitasnya tinggi. Ditarik dari posisi setimbang,pegas mendapat energi potensial elastisnya. Energi ini pula yang mendorong seseorang memantul kembali ke atas.

5. Garpu tala

Perbedaan ukuran garpu tala menyebabkannya menghasilkan titinada yang berbeda pula. Makin besar massa garpu tala semakin rendah frekuensi osilasi dan makin rendah pula nada yang dihasilkan.

6. Jam mekanik

Pada roda keseimbangan dari suatu jam mekanik mempunyai komponen pegas yang akan memperlihatkan suatu torsi pemulih yang sebanding dengan perpindahan sudut dan posisi kesetimbangan. Gerak ini merupakan gerak harmonik sederhana jenis angular.

I. CONTOH SOAL GERAK HARMONIK SEDERHANA

1. Sebuah benda melaksanakan gerak harmonik dengan amplitudo 2A. Pada ketika kecepatannya sama dengan seperempat kecepatan maksimum, tentukan simpangannya!

PENYELESAIAN SOAL 1

2. Saat energi kinetik benda bergetar selaras sama dengan energi potensialnya maka...

PENYELESAIAN SOAL 2

3.Sebuah benda dengan massa 4 gram digetarkan dengan y = 0,05 sin 300t dengan satuan internasional. Tentukan kecepatan dan percepatannya ketika t = 2 s.

PENYELESAIAN SOAL 3

4. Jika massa beban yang digantung pada ujung bawah pegas 3 kg, maka periode getarannya 7 sekon. Jika massa beban dilipat gandakan menjadi 9 kg, maka tentukan periode getarannya!

PENYELESAIAN SOAL 4

Nah itulah beliau pembahasan kami kali ini ihwal Gerak Harmonik Sederhana, biar sanggup bermanfaat bagi sahabat semuanya. Apabila masih ada yang belum dimengerti silahkan sahabat tanyakan melalui kotak komentar di bawah ini, kami akan berusaha merespon dengan cepat dan tepat. Terimakasih telah berkunjung di softilmu, jangan lupa like, follow, dan komentarnya ya J.